Feb 13, 13 · let's see if we can evaluate the indefinite integral one over nine plus x squared DX and we know that if you have the pattern a squared minus x squared it could be a good idea to make the substitution X is equal to a sine theta but we don't see that pattern over here what instead what we see is a squared plus x squared and in this context it tends to be a good idea it's not alwaysFree integral calculator solve indefinite, definite and multiple integrals with all the steps Type in any integral to get the solution, steps and graph This website uses cookies to ensure you get the best experienceWe can use the identity \(\sec^2 \theta = \tan^2 \theta 1\) to help us \\begin{align*} \int_0^{\tfrac{1}{4} \pi} \tan^3 \theta \d\theta &= \int_0^{\tfrac{1}{4

Integral Of The Secant Function Wikipedia
Tan^2 theta integral
Tan^2 theta integral-The angle between the second line and the xaxis is Place P on the line defined by at a unit distance from the origin Let PQ be a line perpendicular to line OQ defined by angle , drawn from point Q on this line to point P OQP is aThe integral yields to standard substitutions Sometime when I am feeling in a clever mood I may come up with a quick to verify solution At this point, I am interested in showing that the integral can be done by absolutely routine substitutions By analyzing the substitutions, we



Get Answer Prove The Given Identity Cos 2 Theta 1 Tan2 Theta 1 Which Transtutors
The definite integral of from to , denoted , is defined to be the signed area between and the axis, from to Both types of integrals are tied together by the fundamental theorem of calculus This states that if is continuous on and is its continuous indefinite integral, then This means Sometimes an approximation to a definite integral isSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreIn mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions In calculus, trigonometric substitution is a technique for evaluating integralsMoreover, one may use the trigonometric identities to simplify certain integrals containing radical expressions Like other methods of integration by substitution, when evaluating a definite integral, it
Evaluate the integral \displaystyle \int \theta \tan^2 \theta\ d \theta Join our free STEM summer bootcamps taught by experts Space is limitedIntegral tan 4x sec^4 4x dx integral tan^4 theta sec^4 theta d theta integral sec^5 x tan^3 x dx integral tan^5 theta sec theta d theta integral tan^4 x sec x dx\\int \tan^{2}x \, dx\ > <
This article uses Greek letters such as alpha (α), beta (β), gamma (γ), and theta (θ) to represent anglesSeveral different units of angle measure are widely used, including degree, radian, and gradian () 1 full circle () = 360 degree = 2 π radian = 400 gonIf not specifically annotated by (°) for degree or for gradian, all values for angles in this article are assumed to be given inMay 26, · In this section we are going to look at some integrals that involve quadratics for which the previous techniques won't work right away In some cases, manipulation of the quadratic needs to be done before we can do the integral We willThe differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variableFor example, the derivative of the sine function is written sin′(a) = cos(a), meaning that the rate of change of sin(x) at a particular angle x = a is given by the cosine of that angle
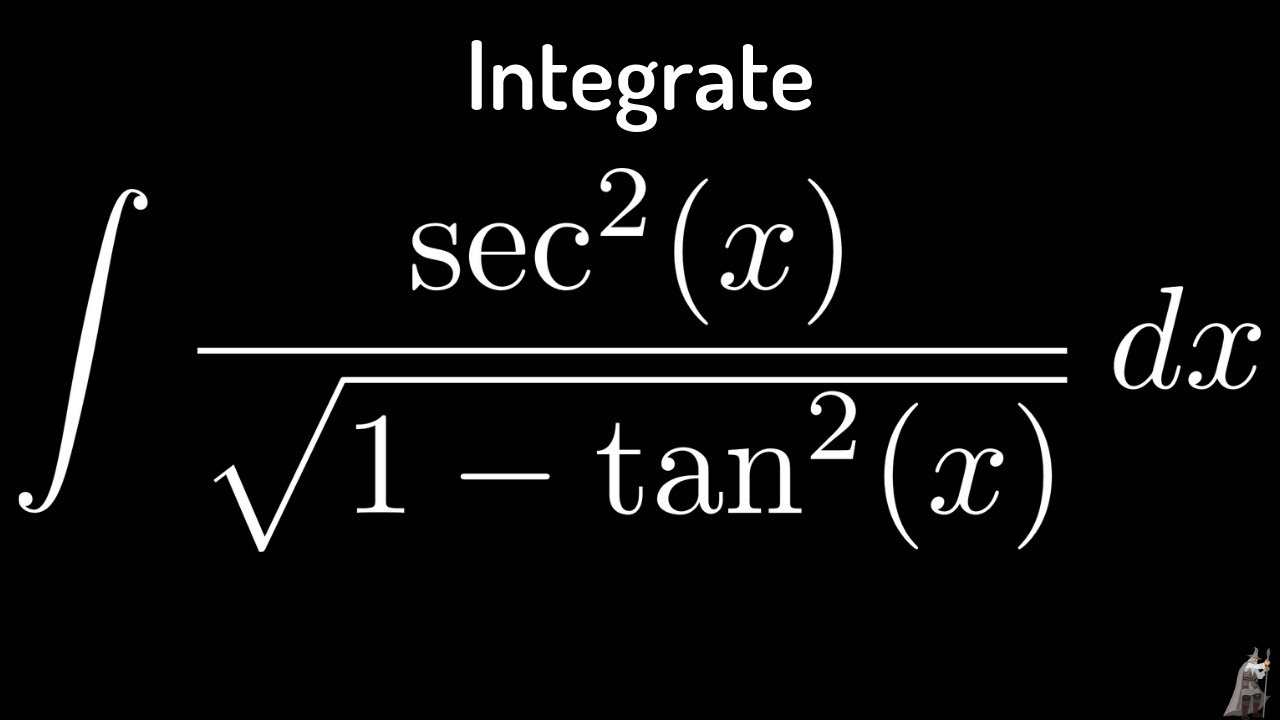


Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube



Question Video Determining Whether The Integrals Of Trigonometric Functions With Exponents Are Convergent Or Divergent Nagwa
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreMar 31, 17 · Here's an alternative approach Note that #tantheta = sin theta/costheta# #sintheta/costheta = sqrt(2)sintheta# Multiply both sides by #costheta# #sintheta/costheta * costheta = sqrt(2)sintheta*costheta# Now recognize that #sin2theta = 2sinthetacostheta# #sintheta = sqrt(2)sinthetacostheta# Multiply the right side by #2/2#With this equation, we're gonna have the integral of the tan of data to the fourth times the tan off Theda squared, plus one times the seek and of data squared Dean data from here, we're just going to, uh, distribute out our cans
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com



V T 910 U03c01 Cos2 U03c0 T 3 Liters F X X 3 5 F X X 5 G X X 3 Cos X 4 Dx U03c0 4 Dx Lnx 28 Xf Course Hero
Draw a horizontal line (the xaxis);Jan 30, 17 · integrate cos^2(theta) * tan^2(theta) d(theta), from theta=0 to pi/4Mark an origin O Draw a line from O at an angle above the horizontal line and a second line at an angle above that;


Trigonometric Substitution Calculus Volume 2



Find The Indefinite Integral Tan 6 3x Dx Homework Help And Answers Slader
Feb , 15 · Integral of tan^2x, solution playlist page http//wwwblackpenredpencom/math/Calculushtmltrig integrals, trigonometric integrals, integralDec 01, · Integration by Trigonometric Substitution Depending on the function we need to integrate, we can use this trigonometric expression asThey use the key relations sin 2 x cos 2 x = 1 \sin^2x \cos^2x = 1 sin 2 x cos 2 x = 1, tan 2 x 1 = sec 2 x \tan^2x 1 = \sec^2x tan 2 x 1 = sec 2 x, and cot 2 x 1 = csc 2 x \cot^2x 1 = \csc^2x cot 2 x 1 = csc 2 x to manipulate an integral into a simpler form The derivatives of trigonometric functions



Integration Of Inverse Tan 2x Integration By Parts Youtube



Trigonometric Substitutions
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepFirst thing, I have been studying maths for business for approximately 3 months now Since then, I studied algebra and then I started studying calculus Yet, my friend stopped me there, and asked me to study Fourier series as we'll need it for our incoming projects So I feel that I am



How To Evaluate Int 0 1 Frac X Ln 1 X Ln 1 X 2 1 X 2 Dx Mathematics Stack Exchange
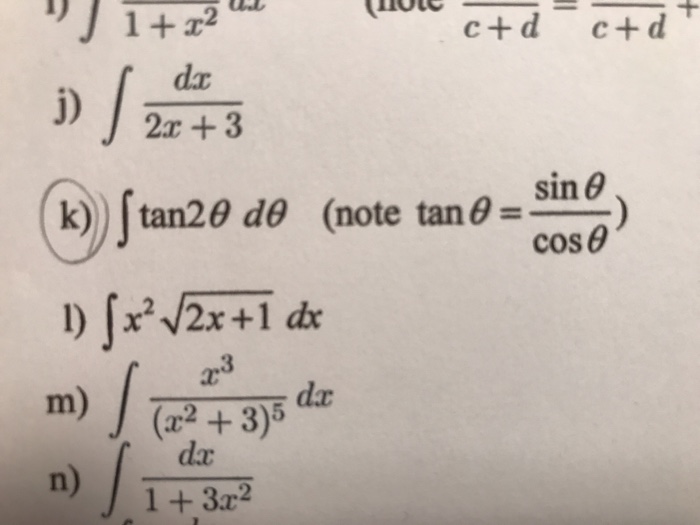


Solved Integral Dx 2x 3 Integral Tan 2 Theta D Theta N Chegg Com
The derivative of a cosine is a sine and thus I integrate the cosine function as if it were an x Now, there is nothing wrong with substitution, I want to make that clear But beyond Calc1, particularly in calc 2 and DFQ, Trouble solving $\int\frac{\sec^2\theta}{\tan^2\theta4}d\theta$ 1 How to solve $ \int \tan{\theta}\sec^4{\theta}dIf ∫ cos 2 θ (tan 2 θ sec 2 θ) d θ = λ tan θ 2 lo g e ∣ f ( θ ) ∣ C where C is a constant of integrating, then the ordered pair ( λ , f ( θ ) ) is equal to APricing Log in Sign up Calculus 1 answer 0 watching 86 views 11 Nov 19 evaluate the integral sec 2 theta tan 2 theta d theta Answer



Hw 02 Spring 17 Key Math 2414 Homework Set 10 Points Pts 2sec Dz 2sec Tan 2sec 1593 4sec 32 Tan 2sec 2810 With These Limits We Know That Tangent Is Positive Studocu



Solved Evaluate The Integrals A Integral E 3x Sin 2x Dx Chegg Com
Jun 16, 19 · Get the detailed answer evaluate the integral sec 2 theta tan 2 theta d theta Get the detailed answer evaluate the integral sec 2 theta tan 2 theta d theta Homework Help What's your question?PROBLEM 26 Integrate Click HERE to see a detailed solution to problem 26 PROBLEM 27 Integrate Click HERE to see a detailed solution to problem 27 Click HERE to return to the original list of various types of calculus problems Your comments and suggestions are welcome Please email any correspondence to Duane Kouba by clicking on theSec 2 theta * tan 2 theta d theta, Evaluate the indefinite integral


How To Integrate X Tan 2 X Dx Quora
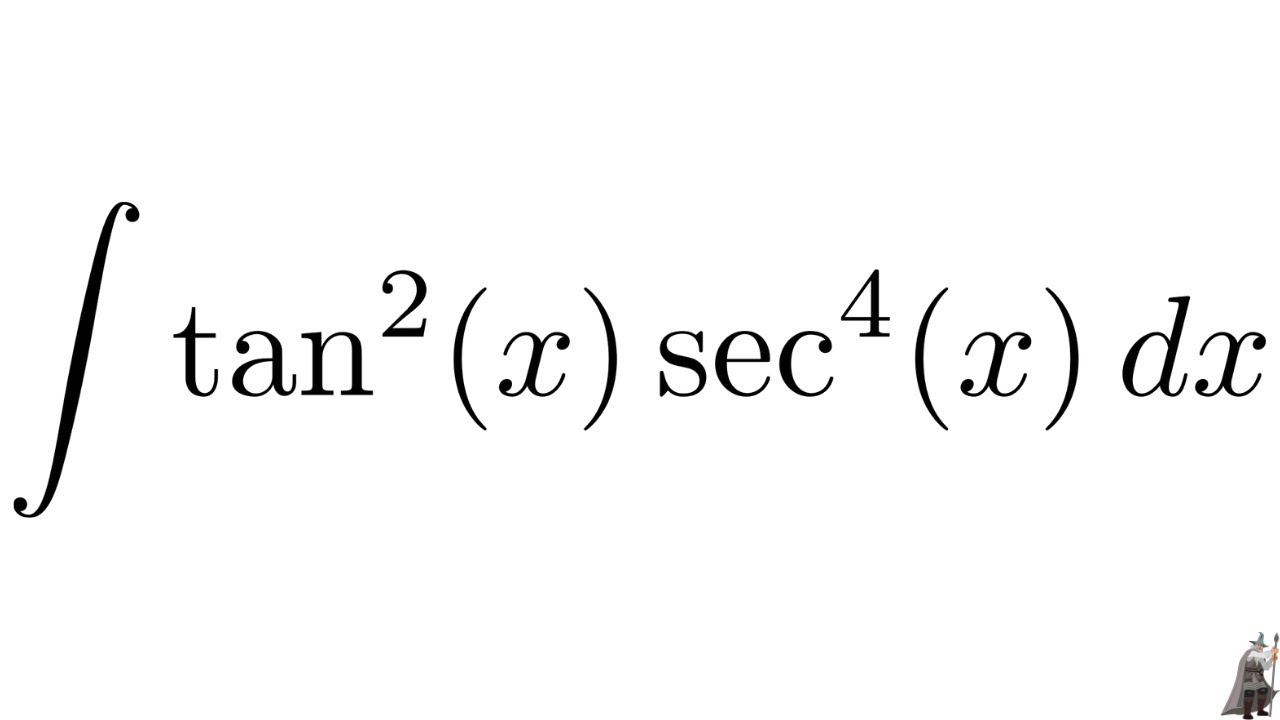


Integral Tan 2 X Sec 4 X Youtube
Jul 31, 18 · How do I integrate $\sin\theta \sin\theta \tan^2\theta$ ?Definite Integral The integral that has both upper and the lower bounds of integration is a definite integral (1 tan^2 \theta)d \theta {/eq} $$\begin{align} \int_0^{\frac{\pi}{3}} (1Solve the integral = ln u C substitute back u=cos x = ln cos x C QED 2 Alternate Form of Result tan x dx = ln cos x C = ln (cos x)1 C = ln sec x C



Integral Tan 2 X Sec X Youtube
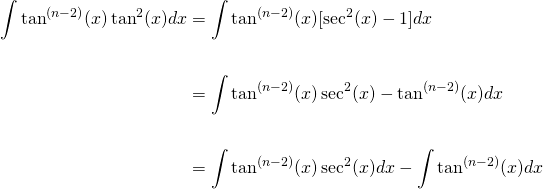


Reduction Formula For The Integral Of Tan N X Dx Steemit
Answer to Compute the following integral sec (theta) tan 2 (theta) d theta By signing up, you'll get thousands of stepbystep solutions to yourQ If $\int \frac{d\theta}{cos^{2}\,\theta\left(tan\,2\thetasec\,2\theta\right)}=$ $\lambda\,tan\theta2\,log_{e}\leftf \left(\theta\right)C\right$ where C is aRecall that if $$ x = f(\theta) \ , $$ $$ dx = f'(\theta) \ d\theta $$ For example, if $$ x = \sec \theta \ , $$ then $$ dx = \sec \theta \tan \theta \ d\theta $$ The goal of trig substitution will be to replace square roots of quadratic expressions or rational powers of the form $ \ \displaystyle \frac{n}{2} \ $ (where $ \ n \ $ is an integer



Integrate Int 1 0 Frac R 3 Sqrt 4 R 2 Dr Mathematics Stack Exchange
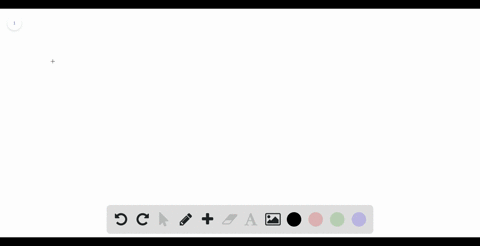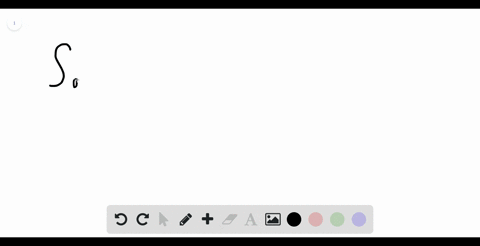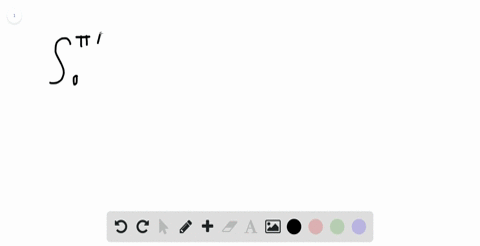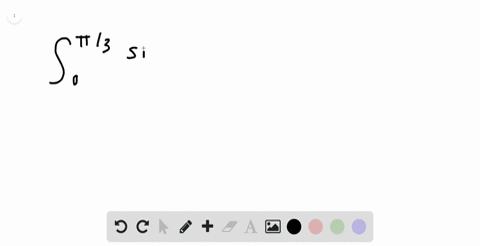


Solved Evaluate The Integral Displaystyle Int
Mar 05, 18 · Evaluate \( \displaystyle \int{{{{\sec }^6}\left( {3y} \right){{\tan }^2}\left( {3y} \right)\,dy}}\) Show All Steps Hide All Steps Hint Pay attention to the exponents and recall that for most of these kinds of problems you'll need to use trig identities to put the integral into a form that allows you to do the integral (usually with a CalcIntegration by Trigonometric Substitution Examples 2 We will now look at some more examples of integration by trigonometric substitution Please look back at the Integration by Trigonometric Substitution Examples 1 for more examples Additionally, recall the following tableJan 13, 17 · tan^2(x)/2ln(abscos(x))C Split up tan^3(x) into tan^2(x)tan(x) then rewrite tan^2(x) using the identity tan^2(theta)1=sec^2(theta)=>tan^2(theta)=sec^2(theta)1 inttan^3(x)dx=inttan^2(x)tan(x)dx=int(sec^2(x)1)tan(x)dx Distribute =intsec^2(x)tan(x)dxinttan(x)dx For the first integral, apply the substitution u=tan(x)=>du=sec^2(x)dx, both of which are already in the integral



Finding The Antiderivative Of 1 Cos X Video Lesson Transcript Study Com



Get Answer Prove The Given Identity Cos 2 Theta 1 Tan2 Theta 1 Which Transtutors
Sep 26, · Note that Integral B is integral A with the substitution ##x=a\tan\theta## Thus terms 1 and 2 in Integral A are the same as terms 1 and 2 in Integral B (term #2 requires some trigonometric manipulation and borrows a factor ##\ln a## from the integration constant)Mar 03, 15 · I'm stuck in this problem I can not integrate $\int \sec\theta\tan^2\theta \,d\theta$ Can anyone help me calculus integration trigonometry Share Cite Follow edited Mar 4 '15 at 056 user asked Mar 3 '15 at 1014 Shahed al mamun Shahed al mamun 171 3May 26, · In this section we will look at integrals (both indefinite and definite) that require the use of a substitutions involving trig functions and how they can be used to simplify certain integrals
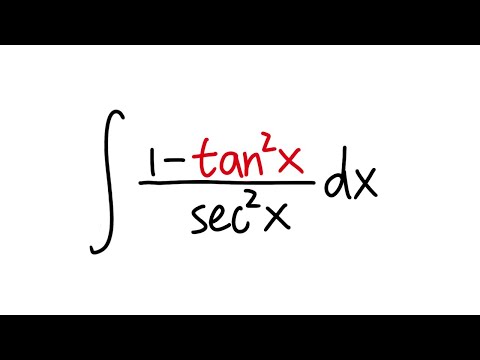


Q45 Integral Of 1 Tan 2x Sec 2x Youtube
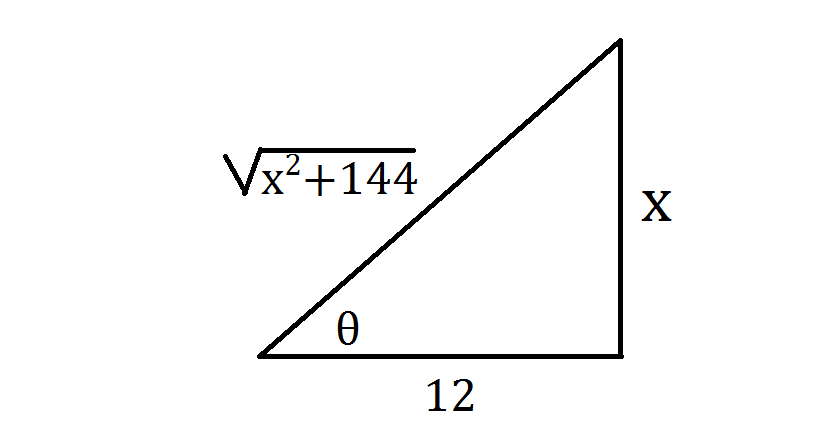


How Do You Integrate Int X Sqrt 144 X 2 Dx Using Trigonometric Substitution Socratic
In various applications of trigonometry, it is useful to rewrite the trigonometric functions (such as sine and cosine) in terms of rational functions of a new variable These identities are known collectively as the tangent halfangle formulae because of the definition of These identities can be useful in calculus for converting rational functions in sine and cosine to functions of t in order



Integrate Cot X Sin X Tan X Cos X 3tan 2 X Dx Maths Integrals Meritnation Com


Evaluate Tanx Tan 3x 1 Tan 3x Dx Sarthaks Econnect Largest Online Education Community



Integrate Sec 2x Method 2



Integral 1 Tan 2 X Sec 2 X Youtube
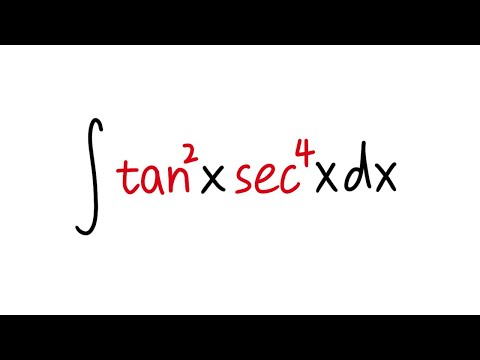


Calculus 7 2 22 Integral Of Tan 2x Sec 4x Youtube


10 4 Integration Of Powers Of Trigonometric Functions
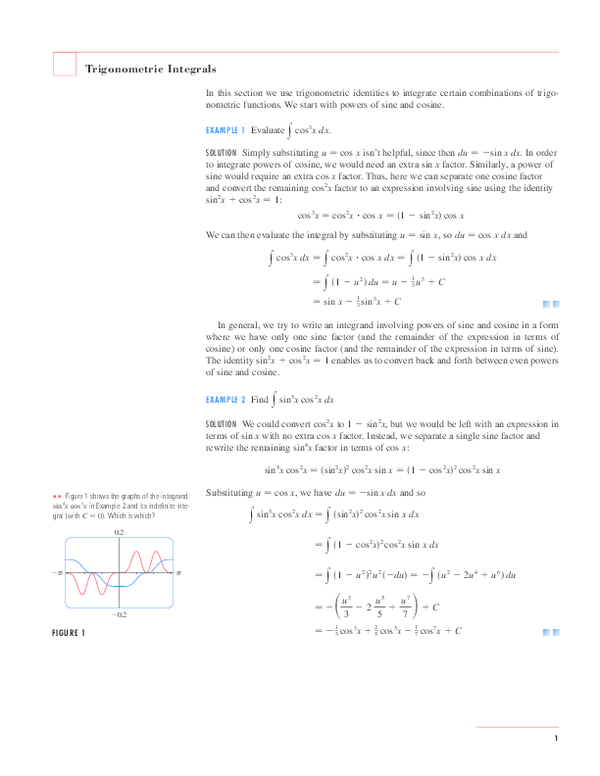


Pdf Trigonometric Integrals Jerome Delen Academia Edu



Integral Of Secant Cubed Wikipedia


Establish Relations For The Integral From 0 To P 4 Of Tann X Stumbling Robot



Integral Of Secant Cubed Wikipedia


7 3 Trigonometric Substitution Mathematics Libretexts



Which Of These Answers Is The Correct Indefinite Integral Using Trig Substitution Or U Substitution Give Different Answers Mathematics Stack Exchange


Trigonometric Substitution



Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55



Powers Of Trigonometric Functions


Integral Of Sec 6 X Tan 2 X Dx



What Function Represented By Graph Answer Choices Y Tan 2 Theta Y Tan 1 2 Theta Y Tan Theta Y Tan Brainly Com



Int 1 Tan 2x 1 Tan 2x Dx
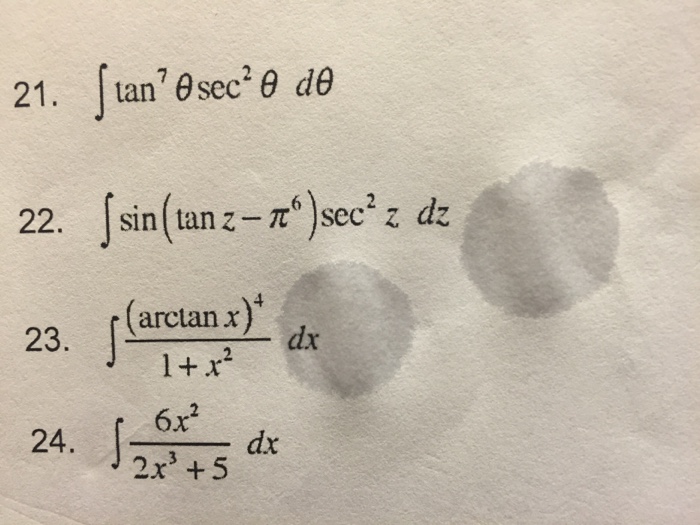


Solved Integral Tan 7 Theta Sec 2 Theta D Theta Integral Chegg Com


What Is The Integration Of Tan Square X Quora



What Is The Integration Of Tan 2x Solution Quora



State Whether The Statement Is True False If Theta Is Not An Integral Multiple Of Pi2 Then Tantheta 2tan 2theta 4tan 4theta 8cot 8theta Cottheta



Trigonometric Substitution Wikipedia Republished Wiki 2


Trigonometric Integrals



Integrate Tanx Tan 2x Tan3x Dx Maths Integrals Meritnation Com



Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous



Integral Of The Secant Function Wikipedia



Can I Integrate Math Tan 2 X Sec 3 X Math Using The Substitution Quora



If Theta Is Not An Integral Multiple Of Frac Pi 2 Prove That Tan Theta 2 Tan 2 Theta 4 Tan 4 Theta 8 Cot 8 Theta Cot Theta 33



Integrate Tan 2x



How Do You Integrate Int Sec 2theta Sintheta D Theta Socratic



Solving The Integral Of Cos X Video Lesson Transcript Study Com



Integral 2



Solved Evaluate The Integral Integral 5pi 3 0 2 Sin Thet Chegg Com



Solved Integrate Sqrt 1 Tan 2 X Dx Between Pi 4 Chegg Com



Integral Of Tan 2 X Youtube



Solved Integral Infinity 1 E 1 X X 2 Dx Integral Tan 2 T Chegg Com
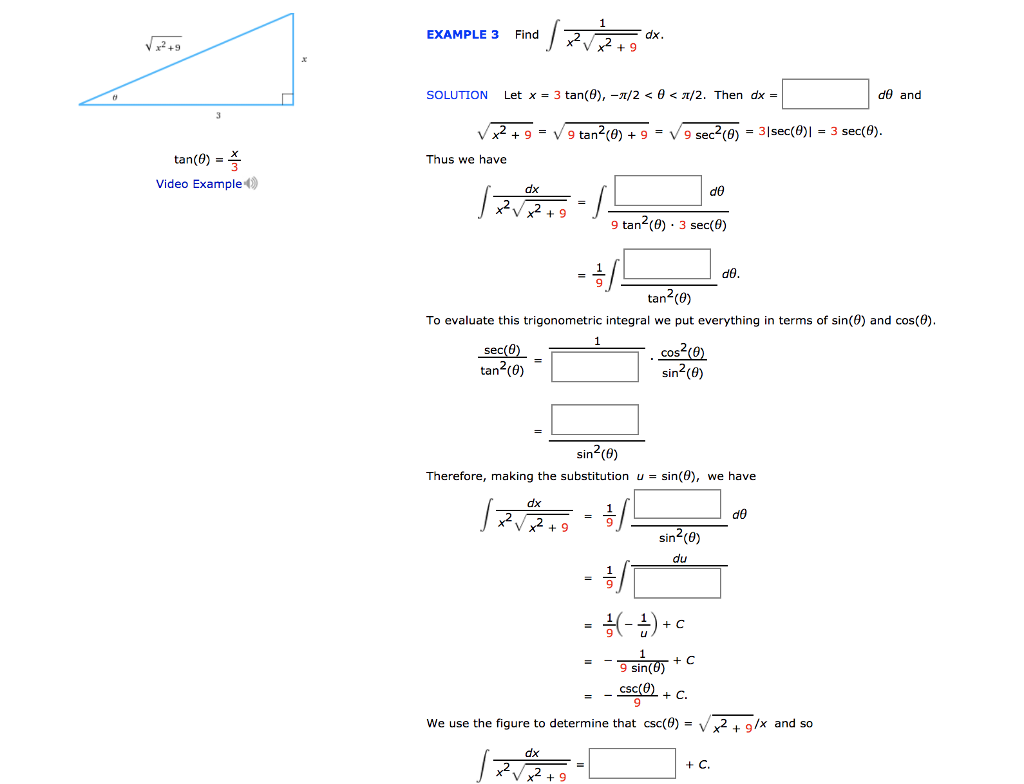


Solved Example 3 Find9 Dx Solution Let X 3 Tan 8 Z 2 8 Chegg Com



Integral Of Tan 2x Youtube



The Integral Int Sec 2x Secx Tanx 9 2 Dx Equals For Some


Trigonometric Substitution



Integral Of Tan 3 X Dx Where Did I Go Wrong Math Help Forum



How Do You Integrate 1 Tan2x Sec2x Dx Socratic



Oneclass Evaluate The Integral Sec 2 Theta Tan 2 Theta D Theta
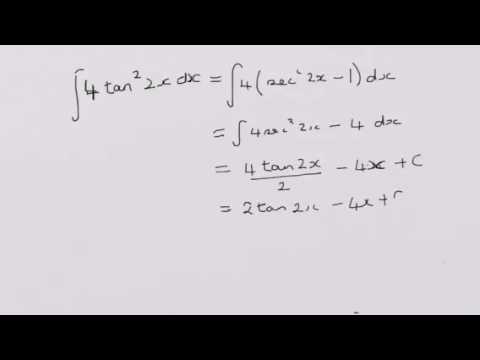


Integrating Tan 2 2x Youtube
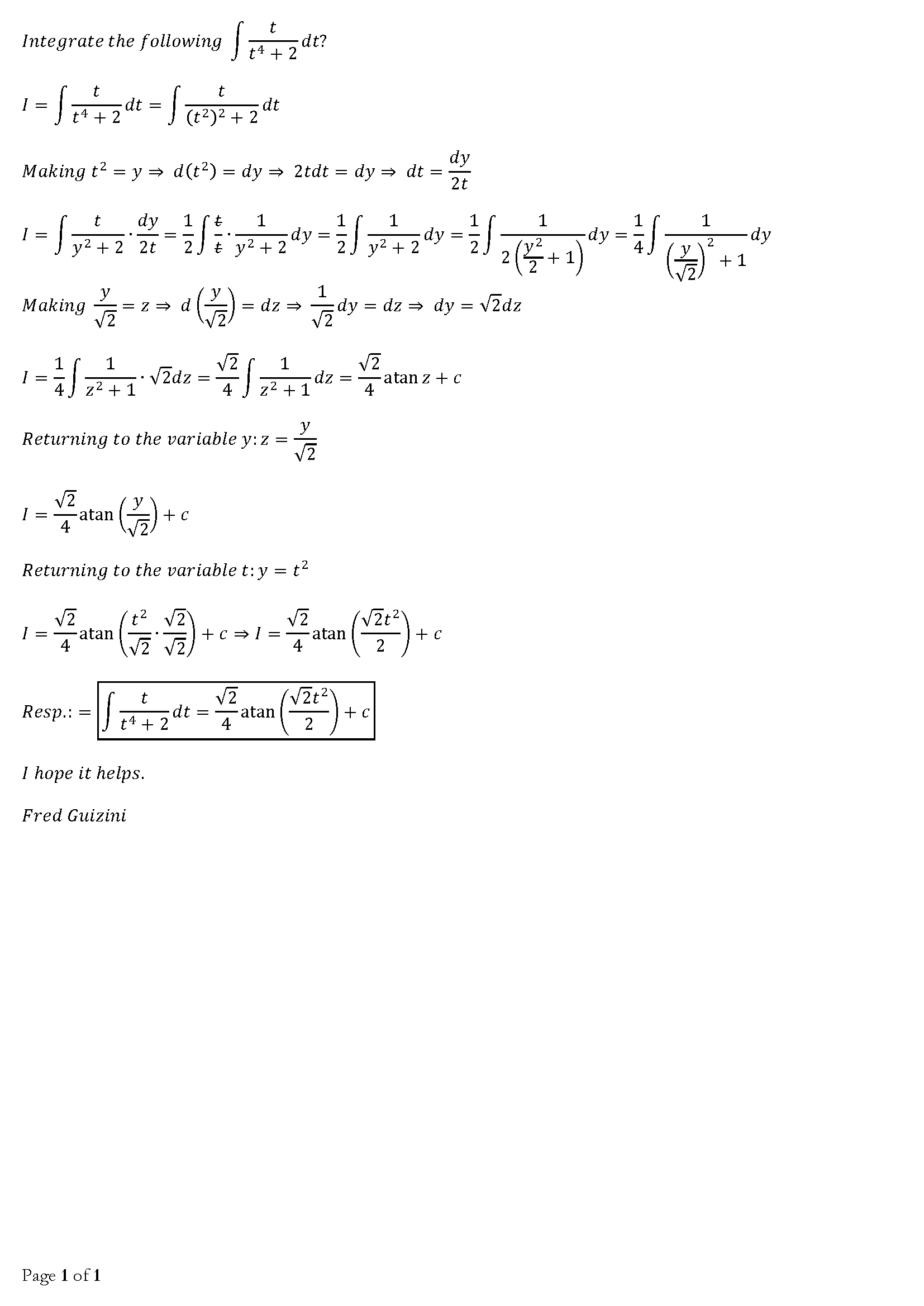


Integrate The Following Int T T 4 2 Dt Socratic



Ex 7 4 9 Integrate Sec 2 X Root Tan 2 X 4 Ncert Class 12
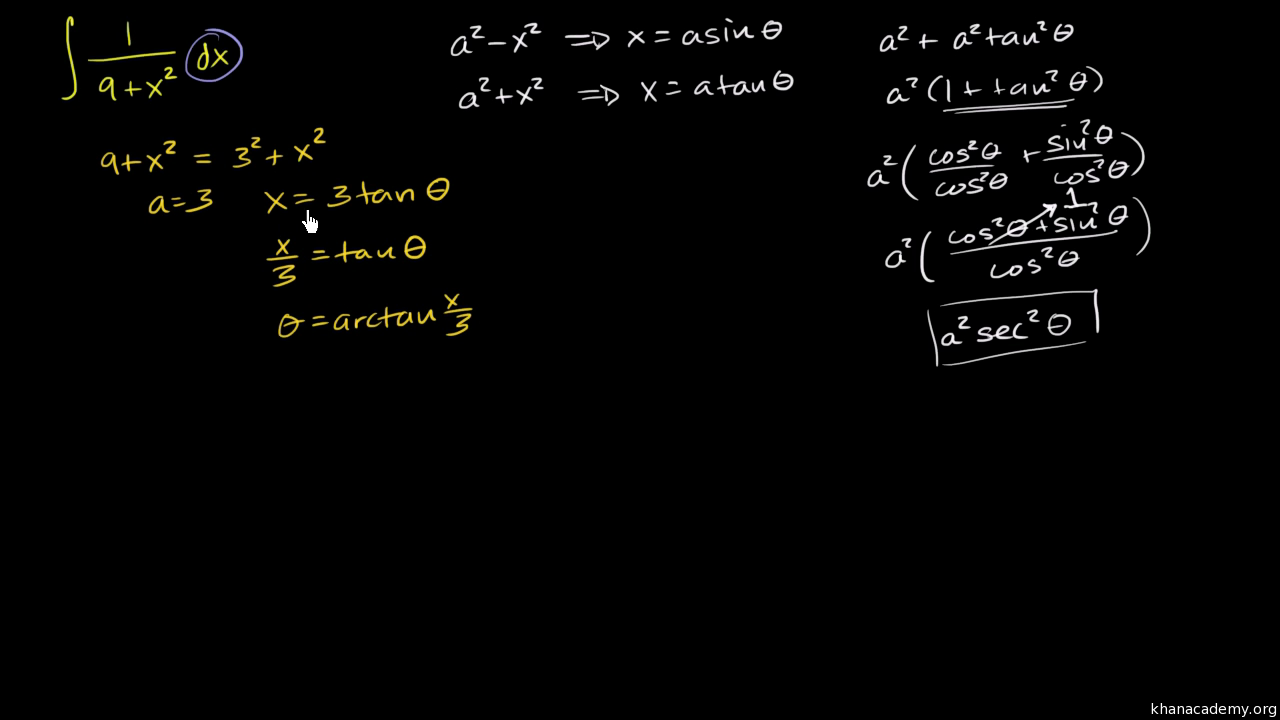


Trig Substitution With Tangent Video Khan Academy



By Parts Integration By Parts Although Integration By Parts Is Used Most Of The Time On Products Of The Form Described Above It Is Sometimes Effective Ppt Download


Trigonometric Integrals
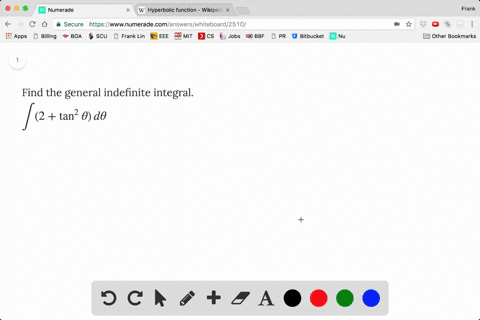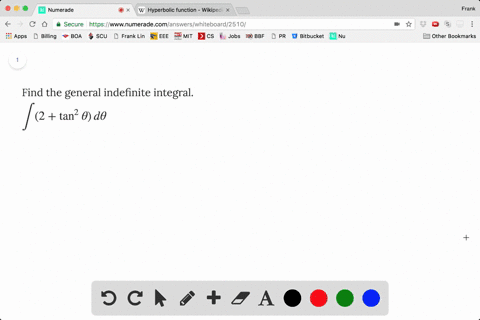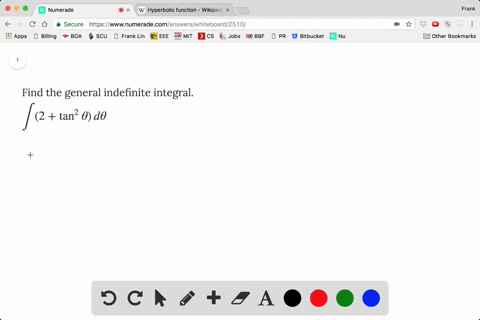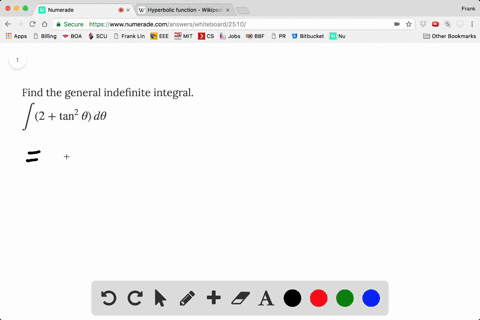


Solved Find The General Indefinite Integral Dis



Calculus Integration Techniques Trigonometric Substitution Wikibooks Open Books For An Open World



Weierstrass Substitution Wikipedia


10 4 Integration Of Powers Of Trigonometric Functions



Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2


How Do I Integrate Tan 2 X Youtube



Integration Of Tan 2 X Sec 2 X Youtube



Trig Substitution With Tangent Video Khan Academy


How To Integrate Tan 2x Youtube



For Theta In 0 Pi 2 The Value Of Definite Integral Int 0 Theta L



Evaluate Int 0 Pi 4 Tan 2 X Dx


Trigonometric Substitution


What Is The Integration Of Tan Square X Quora
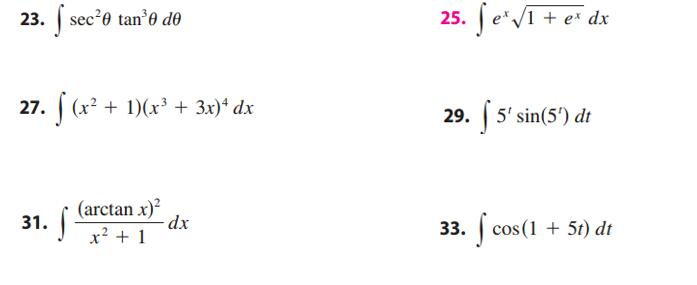


Solved Integral Sec 2 Theta Tan 3 Theta D Theta Integral Chegg Com
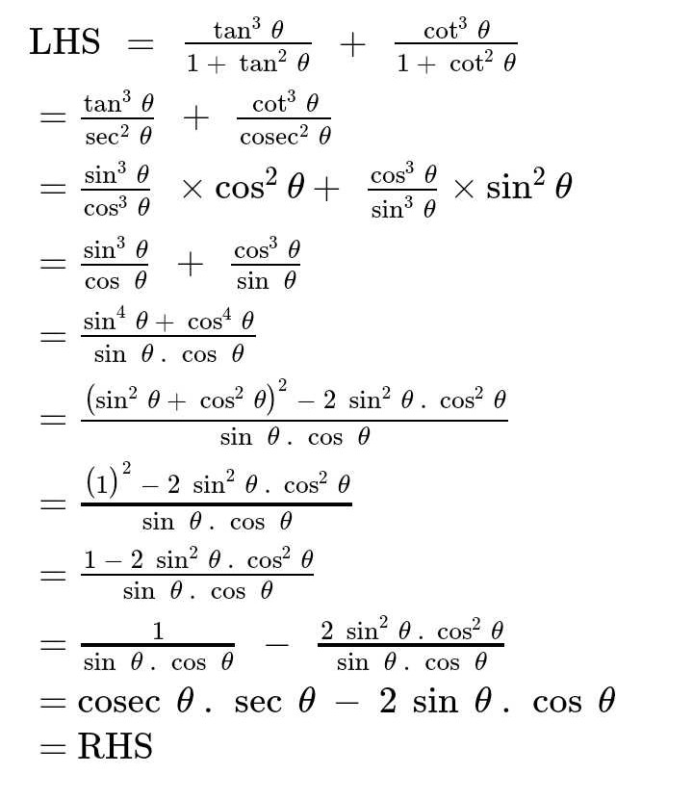


Prove If Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Cosec Theta 2 Sin Theta Cos Theta Edurev Class 10 Question



Integral Of The Secant Function Wikipedia



Weierstrass Substitution Wikipedia



Integrate Cosec 2x


Evaluate Tan 2 X Dx For X 0 P 4 Sarthaks Econnect Largest Online Education Community



Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download



How To Integrate Math Int Sin 4x Cdot E Tan 2x Dx Math Quora



Ex 7 2 21 Integrate Tan2 2x 3 Class 12 Cbse Ex 7 2



Solved Evaluate Integral Tan 6 2x Sec 4 2x Dx If We Chegg Com



Answered 12z2 Evaluate The Integral A Which Bartleby


Integral Of Sec 6 X Tan 2 X Dx



Weierstrass Substitution Wikipedia



Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous
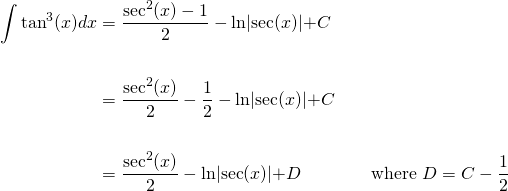


Integral Of Tan 3 X Steemit



0 件のコメント:
コメントを投稿